Брызги от колеса. Задача с решением
Задача о брызгах от колеса, с подробным решением.
Задача. Телега катится по горизонтальной мокрой дороге. На которую максимальную высоту поднимаются капли воды, отрывающейся от колес?
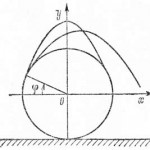 Решение. Самая существенная особенность этой задачи заключается, пожалуй, в том, что для её решения нельзя поместить начало координат в исходную точку траектории капли, так как отрыв капель происходит в разных точках обода колеса. Совместим поэтому начало координат с центром колеса, т.е. будем рассматривать движение капель в системе отсчета, связанной с телегой, движущейся равномерно и прямолинейно относительно земли. Очевидно, что максимальная высота подъема капель по вертикали не зависит от того, рассматривать их движение в системе отсчета, связанной с землей, или в системе отсчета, связанной с равномерно движущейся по горизонтали телегой. Если скорость телеги равна v0 и колеса не пробуксовывают, то в выбранной системе отсчета величина скорости любой точки обода также равна v0. Положение любой из точек, в которых происходит отрыв капли от обода, однозначно определяется углом ? (рисунок).
Решение. Самая существенная особенность этой задачи заключается, пожалуй, в том, что для её решения нельзя поместить начало координат в исходную точку траектории капли, так как отрыв капель происходит в разных точках обода колеса. Совместим поэтому начало координат с центром колеса, т.е. будем рассматривать движение капель в системе отсчета, связанной с телегой, движущейся равномерно и прямолинейно относительно земли. Очевидно, что максимальная высота подъема капель по вертикали не зависит от того, рассматривать их движение в системе отсчета, связанной с землей, или в системе отсчета, связанной с равномерно движущейся по горизонтали телегой. Если скорость телеги равна v0 и колеса не пробуксовывают, то в выбранной системе отсчета величина скорости любой точки обода также равна v0. Положение любой из точек, в которых происходит отрыв капли от обода, однозначно определяется углом ? (рисунок).
Текущие координаты капли, оторвавшейся в точке, характеризуемой углом ?, определяются соотношениями:
(1)
(2)
Для нахождения максимальной высоты подъема капли ymax нужно подставить в уравнение (2) время подъема капли t1, которое проще всего найти следующим образом. В наивысшей точке траектории вертикальная составляющая скорости vy обращается в нуль: vy=v0cos? — gt1=0, откуда
(3)
Тогда максимальная высота подъема капли, оторвавшиеся от обода в рассматриваемой точке,
(4)
(В этой формуле cos? выражен через sin?.)
Из (4) видно, что максимальная высота подъема зависит от угла ?, т.е. от того, в какой точке произошел отрыв капли. В такой же точке должна оторваться капля, чтобы подняться выше всех остальных? Выражение (4) для максимальной высоты подъема представляет собой квадратный трехчлен относительно sin? и принимает свое наибольшее значение.
(5)
при ![]() Конечно, этот результат имеет смысл, если
Конечно, этот результат имеет смысл, если ![]() , т.е. если телега катится достаточно быстро. В противном случае, как нетрудно убедиться, ни одна из отрывающихся капель не поднимается выше верхней точки обода.
, т.е. если телега катится достаточно быстро. В противном случае, как нетрудно убедиться, ни одна из отрывающихся капель не поднимается выше верхней точки обода.
С помощью соотношения (1) легко увидеть, что найденная точка наивысшего подъема лежит точно над осью колеса: подставляя (3) в (1) и учитывая, что ![]() , получаем x=0.
, получаем x=0.
Ответ на поставленный в задаче вопрос — формула (5) для наибольшей высоты подъема отрывающихся капель — получен путем исследования на максимум квадратного трехчлена (4) относительно sin?. Этот результат можно получить и иначе. Будем рассуждать следующим образом. Будем рассуждать следующим образом. Зафиксируем некоторое значение ymax и решим уравнение (4) относительно sin?:
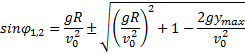
(6)
Здесь углы ?1 и ?2 определяют те точки обода, отрываясь от которых капли достигают заданной максимальной высоты. Если вещественных корней нет, то заданного значения ymax не достигает ни одна капля. Если есть два различных вещественных корня ?1 и ?2, то заданная высота является максимально для двух капель. Наибольшей высоты, из всех капель, как видно из того же рисунка, достигает только одна капля. Следовательно, эту наибольшую высоту hmax можно найти, потребовав, чтобы оба корня уравнения (6) сливались в один: приравнивая дискриминант нулю, получаем ответ — формулу (5).
Итак, получено исчерпывающее решение этой задачи. Мы решали ее, используя уравнения движения (1) и (2), которые дают зависимость координат движущегося тела от времени. Эти уравнения содержат всю информацию о движении тела. Но во многих случаях полная информация бывает не нужна. Например, в обсуждаемой задаче нас совершенно не интересуют временные зависимости — требуется найти лишь положение точки наивысшего подъема капли, а момент времени, когда капля там оказывается, интереса не представляет. В подобных случаях часто оказывается удобным с самого начала исключить избыточную информацию, воспользовавшись законами сохранения. В рассматриваемой задаче можно сразу получить соотношение (4) для наибольшей высоты подъема капель, если применить закон сохранения механической энергии. Полагая потенциальную энергию капли на уровне оси колеса равной нулю, для полной энергии капли в точке отрыва имеем:
![]() В высшей точке траектории вертикальная составляющая скорости обращается в нуль. Поскольку горизонтальная составляющая скорости не меняется, энергия в высшей точке
В высшей точке траектории вертикальная составляющая скорости обращается в нуль. Поскольку горизонтальная составляющая скорости не меняется, энергия в высшей точке
![]() Приравнивая E1 и E2, получаем формулу (4). Как видите, во многих задачах не вредно подумать о том, нельзя ли упростить решение, используя законы сохранения!
Приравнивая E1 и E2, получаем формулу (4). Как видите, во многих задачах не вредно подумать о том, нельзя ли упростить решение, используя законы сохранения!
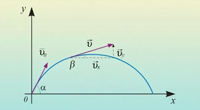 Задача на баллистическое движение с решением
Задача на баллистическое движение с решением