Кинематика. Баллистическое движение. Задача с решением

Продолжая рассматривать раздел «Кинематика». Предлагаю вам задачу с решением.

Задача. Зенитное орудие может сообщить снаряду начальную скорость v₀ в любом направлении. Требуется найти границу, отделяющую цели, до которых снаряд и данного орудия может долететь, от недостижимых целей. Сопротивлением воздуха пренебречь.

Решение. Попробуем сначала выяснить, что можно сказать об этой границе, не решая задачи. Сам факт существования этой границы сомнений не вызывает, так что поставленный в задаче вопрос имеет смысл (кстати, начиная решать задачу, никогда не вредно подумать об этом). Попытаемся представить себе искомую границу. Очевидно, что она представляет над орудием, то стрелять нужно вертикально вверх. Снаряд при этом понимается на высоту , после чего начинает падать вниз,

так что граница достижимых целей пересекает вертикаль в точке, находящейся на высоте h.

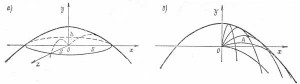
Если ограничиться целями, находящимися на горизонтальной плоскости, то очевидно, что граница представляет собой окружность, радиус которой равен максимально дальности полета снаряда по горизонтали (напоминаем, что максимальная дальность полета по горизонтали достигается при угле возвышения ствола орудия ?=45°). Эта окружность есть пересечение искомой поверхности с горизонтальной плоскостью (рисунок а). Вообще из симметрии можно сделать вывод, что искомая поверхность представляет собой поверхность вращения некоторой кривой вокруг вертикали, проходящей через орудие, и задача сводится к нахождению этой кривой. Отметим, что эта кривая есть огибающая всех возможных траекторий (рисунок б).

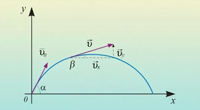
Приступим к решению задачи. Выберем систему координат: орудие расположим в начале координат, ось x направим горизонтально, ось y — вертикально. Тогда зависимость координат снаряда от времени выразится следующим образом:

x(t)=(v₀cos?)t,
y(t)=(v₀sin?)t — gt²/2.

Исключив из этих уравнений t, получим уравнение траектории снаряда y=f(x):

(1)

Это уравнение параболы. Коэффициенты при x и x² зависят от угла ?, т.е. при разных направлениях начальной скорости получаются различные траектории. Таким образом, данное уравнение описывает семейство траекторий при одной и той же величине, но различных направлениях начальной скорости v₀.

Но этому же уравнению можно придать и другой смысл. Будем теперь рассматривать x и y как координаты определенной цели, в которую попадает снаряд, двигаясь по некоторой траектории. Тогда при заданных координатах цели x и y уравнение (1) определяет угол, под которым нужно выпустить снаряд с начальной скоростью v₀ для того, чтобы он попал в эту цель. Решая это квадратное относительно tg? уравнение, находим

(2)

Если уравнение имеет вещественное решение, т.е. дискриминант неотрицателен:

(3)

То в цель попасть можно. Если вещественных решений нет, т.е.

то в цель попасть нельзя. Это значит, что цель находится за пределами искомой границы. Координаты цели, находящейся на границе, удовлетворят соотношению:

Выражая отсюда y как функцию x, получаем уравнение границы в явном виде:

(4)

Это уравнение параболы с вершиной при x=0, . Коэффициент при x² отрицателен, т.е. ветви направлены вниз и пересекают горизонтальную ось в точках (рисунок б). Итак, полученная граница действительно проходит через точки, которые были нами установлены из элементарных соображений. Мы нашли сечение граничной поверхности вертикальной плоскостью, проходящей через начало координат. Вся поверхность может быть получена вращением этой параболы вокруг оси y.

В связи с приведенным решением сделаем еще несколько замечаний. Рассмотрим какую-либо точку, находящуюся ближе границы (например, точку А на рисунке б). Для такой точки подкоренное выражение в формуле (2) положительно, и, следовательно, через нее проходят две траектории (при заданной величине начальной скорости), соответствующие двум возможным значениям угла ?.

В баллистике одна из этих траекторий называется настильной, а другая, касающаяся границы до попадания в цель, — навесной. Через каждую точку, принадлежащую границе, проходит лишь одна траектория. Отметим, что граница является огибающей для семейства траекторий при различных направлениях начальной скорости и фиксированном значении величины начальной скорости v₀.

Приведем другой возможный путь решения этой задачи, связанный с еще одной трактовкой уравнения (1). Рассмотрим цели, находящиеся на одной вертикали, отстоящей от орудия на расстоянии х, и найдем на ней самую высокую точку, в которую еще может попасть снаряд. Эта точка, очевидно, принадлежит границе. Таким образом, задача сводится к нахождению максимума y, т.е. правой части уравнения (1), рассматриваемой как функция угла ?. Правая часть есть квадратный трехчлен относительно tg? и имеет максимум при .