Кинематика
Кинематика изучает «геометрию» движения. Что мы под этим понимаем? «Геометрия» движения — это математическое описание движения без анализа причин, его вызывающих. Другими словами, без выяснения вопроса, почему рассматриваемое движение происходит именно так, а не иначе, устанавливается математическое соотношение между его различными характеристиками, такими, как перемещение, пройденный путь, скорость, ускорение, время движения.
Движение материально точки всегда рассматривается в какой-либо системе отсчета. Положение материальной точки можно определить, если задать её радиус-вектор r или, что эквивалентно, задать три координаты x, y, z — проекции радиус-вектора на оси. Движением математически описано полностью, если известен радиус-вектор как функция времени r(t), т.е. известны три скалярные функции x(t), y(t), z(t). Основной физический закон кинематики устанавливает вид этой функции r(t). Например, для равномерного движения, т.е. движения с постоянной скоростью v, функция r(t) имеет вид:
r(t)=r0+vt, (1)
а для равнопеременного движения с ускорением a:
r(t)=r0+v0t+at2/2. (2)
В этих формулах r0 характеризует начальное положение точки, т.е. r0=r(t) |t=0 = r(0); v0 — начальная скорость.
Подчеркнем, что в кинематике ускорение считается заданным. Величина ускорения находится либо опытным путем, либо расчетным с помощью законов динамики, когда исследуются причины, определяющие характер движения. Забегая вперед, отметим, что уравнение (1) описывает движение материальной точки в инерциальной системе отсчета, если на точку не действуют силы (или все действующие силы уравновешиваются), а уравнение (2) — если действующие силы постоянны. В последнем случае говорят, что движение тела происходит в постоянном во времени однородном силовом поле. Примером такого поля может служить поле тяготения вблизи поверхности Земли при условии, что высота тела над поверхностью мала по сравнению с радиусом Земли. Разумеется, движение тела вблизи поверхности Земли описывается уравнением (2) только тогда, когда можно не учитывать сопротивление воздуха.
Итак, функция r(t) содержит полную информацию о кинематике движения тела, т.е. ответ на любой вопрос в кинематических задачах можно получить, используя только зависимость r(t). Никаких других физических законов при этом привлекать не требуется. Например, зависимость мгновенной скорости точки от времени в однородном поле может быть получена из (2) и иметь вид v(t)=v0+at.
При решении задач мы будет записывать уравнение (2) непосредственно в проекциях на оси координат. При постоянном ускорении a всегда можно выбрать систему координат таким образом, чтобы уравнение (2) сводилось к двум скалярным: так как траектория, по которой движется тело, плоская, то нужно просто совместить, например, плоскость xy с плоскостью, в которой лежит траектория. Тогда векторное уравнение (2) эквивалентно двум скалярным уравнениям:
x(t)=x0+v0xt+at2/2,
y(t)=y0+v0yt+ayt2/2. (3)
В частности, если рассматривать движение тела вблизи поверхности Земли под действием только силы тяжести, то удобно направить ось y вертикально вверх. Тогда вектор ускорения имеет только одну отличную от нуля проекцию: ax=0, ay=—g, и система (3) принимает вид:
x(t)=x0+v0xt=x0+(v0cos?)t,
y(t)=y0+v0yt—gt2/2=y0+(v0sin?)t—gt2/2,
где ? — угол, образованный вектором начальной скорости с горизонтом. Иногда удобно поместить начало координат в начальную точку траектории, тогда x0=y0=0.
Решение любой кинематической задачи сводится к использованию указанных выше уравнений в конкретных условиях, сформулированных в задаче. При этом было бы наивно пытаться овладеть каким-то «общим методом» решения, пригодным для всех задач; подобного «общего метода» попросту не существует. Наоборот, на разбираемых примерах читатель может убедиться, что всегда существует несколько более или менее различающихся между собой подходов к исследованию изучаемых явлений.
Различные подходы нередко оттеняют новые стороны изучаемого явления, позволяя глубже проникнуть в его физический смысл. Поэтому в большинстве разбираемых задач авторы сознательно приводят различные варианты решения. Иногда это использование существенно различающихся подходов к решению сходных задач. Разумеется, в каждом конкретном случае существует оптимальный подход, наиболее быстро приводящий к ответу на вопросы задачи.
Такой многосторонний анализ, использующий разные точки зрения, является чрезвычайно полезным.
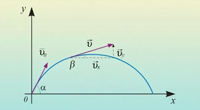 Кинематика. Баллистическое движение. Задача с решением
Кинематика. Баллистическое движение. Задача с решением Брызги от колеса. Задача с решением
Брызги от колеса. Задача с решением