Условие попадания в цель при баллистическом движении. Задача
Условие попадания в цель при баллистическом движении. Очень хорошая задача по кинематике.
Задача. Необходимо с земли попасть камнем в цель с расстояния S. Цель расположена на высоте h. При какой наименьшей начальной скорости камня можно это сделать?
Решение. На первый взгляд кажется, что начальная скорость полета камня будет наименьшей из всех возможных, если наивысшая точка траектории придется на то место, в которое хотим попасть (рисунок а).
Может быть и Вам так показалось? Однако даже не решая задачи, легко убедиться, что это не так. Действительно, будем мысленно уменьшать высоту, на которой расположена цель. При этом точка, куда попадает камень, продолжает согласно предположению оставаться наивысшей точкой траектории (рисунок б), в том числе и в предельном случае h=0. Но совершенно очевидно, что для того, чтобы попасть в цель находящуюся на земле, достаточно просто добросить камень до цели (рисунок б). Итак, предположение о том, что цель совпадает с высшей точкой траектории, несправедливо.
Ошибочность этого предположения становится тем более очевидной, если заметить, что требуемая при этом начальная скорость должна возрастать по мере того, как h?0.
Приведенный анализ представляет собой пример проверки решения задачи предельным переходом к более простому случаю, когда ответ либо очевиден, либо может быть легко найден.
Из рассмотренного примера можно сделать заключение, что цель всегда должна находиться на нисходящей ветви траектории (рисунок в). Еще раз напомним, что мы ищем траекторию с минимальной начальной скоростью.
Приступим к решению задачи.
Пусть камень брошен под углом ? к горизонту и попал в цель. Его перемещения по горизонтали S и по вертикали h могут быть записаны следующим образом:
S=(v0cos?)t,
H=(v0sin?)t — gt2/2.
Поскольку время полета камня t нас не интересует, исключим его из этих уравнений. Выражая t из первого уравнения и подставляя во второе, получаем:
(1)
Это уравнение содержит две неизвестные величины v0 и ? и имеет по этому бесчисленное множество решений, что соответствует возможности попасть в цель бесконечным числом способов. Из этих решений нам нужно выбрать то, которое соответствует минимальному значению v0. Прямой путь решения этой задачи состоит в нахождении v0 как функции от ? из уравнения (1) и исследовании этой функции на экстремум, что требует, однако, применения высшей математики. Поэтому поступим иначе. Попробуем решить уравнение (1) относительно ?. Использую известное соотношение 1/cos2?=1+tg2?, замечаем, что из (1) получается квадратное уравнение относительно tg?:
(2)
Решив его, получим
![]() Казалось бы, ничего хорошего не получается — очень громоздкое выражение. А на самом деле мы в двух шагах от ответа на вопрос задачи. Действительно, для tg? физический смысл имеют только вещественные решения, и поэтому дискриминант должен быть неотрицательным:
Казалось бы, ничего хорошего не получается — очень громоздкое выражение. А на самом деле мы в двух шагах от ответа на вопрос задачи. Действительно, для tg? физический смысл имеют только вещественные решения, и поэтому дискриминант должен быть неотрицательным:
![]() Легко убедиться, что минимальное значение
Легко убедиться, что минимальное значение ![]() , при котором это соотношение справедливо, соответствует случаю равенства; таким образом,
, при котором это соотношение справедливо, соответствует случаю равенства; таким образом,
![]()
Второй корень не имеет физического смысла, так как квадрат скорости есть величина положительная.
Мы получаем ответ ![]() .
.
Проанализируем теперь решение несколько подробнее. Возвратимся к квадратному уравнению для tg?. При положительном дискриминанте оно имеет два решения, т.е. при заданном значении v0 камень может попасть в цель по двум различным траекториям. При отрицательном дискриминанте решений нет, т.е. ни при каком значении угла ? камень не попадет в цель при заданной скорости. При равном нулю дискриминанте имеется только одно решение (единственная траектория полета камня до цели); именно в этом случае, как мы выяснили, начальная скорость будет минимальной. В этом случает выражение для tg? имеет особенно простой вид:
![]()
Проверим правильность полученного результата предельными переходами.
1. Если h=0, то tg?=1, т.е. камень нужно бросить под углом 45°. Хорошо известно, что это соответствует максимальной дальности полета по горизонтали при заданной начальной скорости, т.е. при заданной дальности —минимальной начальной скорости. Этот случай уже обсуждался вначале.
2. Если S?0, то tg???, а ???/2. Действительно, в этом случае камень нужно бросать вертикально вверх, и только в этом случае положение цели совпадает с наивысшей точкой траектории.
Итак, мы решили эту задачу, потребовав, чтобы корни квадратного уравнения (2) для tg? имели физический смысл, т.е. были вещественными.
Рассмотрим теперь несколько иной способ рассуждений, приводящий, естественно, к тому же результату.
Прежде всего отметим одно очевидное обстоятельство: при заданном расстоянии S чем выше расположена цель, тем больше должна быть минимальная начальная скорость камня. Поэтому вместо того чтобы искать минимум v0 при заданном h, можно искать максимум h при заданном v0.
Предположим, что v0 задано. Тогда, выразив h из (2):
![]() легко исследовать получившийся квадратный трехчлен относительно tg? на максимум. (Напомним, что максим квадратного трехчлена y=ax2+bx+с (a<0) имеет место при x=—b/(2a) и равен c — b2/(4a).) Максимальное значение h достигается при
легко исследовать получившийся квадратный трехчлен относительно tg? на максимум. (Напомним, что максим квадратного трехчлена y=ax2+bx+с (a<0) имеет место при x=—b/(2a) и равен c — b2/(4a).) Максимальное значение h достигается при
![]()
и равно
(4)
Из (4) находим минимально значение начальной скорости v0 при заданной высоте цели h, совпадающее с полученным ранее.

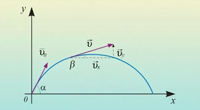 Кинематика. Баллистическое движение. Задача с решением
Кинематика. Баллистическое движение. Задача с решением Брызги от колеса. Задача с решением
Брызги от колеса. Задача с решением