Задача на баллистическое движение с решением

В данном посте для вас задача на баллистическое движение, а так же её подробное решение.

Задача. Между целью и минометом, находящимися на одной горизонтали, расположена стена высотой h. Расстояние от миномета до стены равно a, а от стены до цели b. Определить минимальную величину начальной скорости мины. Под каким углом при этом следует стрелять? Сопротивлением воздуха пренебречь.

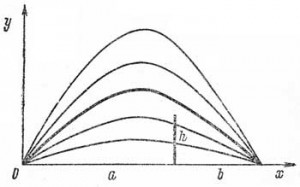Решение. Попробуем разобраться в этой задаче, не выписывая пока никаких формул. Рассмотрим все траектории, проходящие через цель (рисунок), забыв на время о существовании стены. На этом рисунке выделена траектория, соответствующая наименьшему значению начальной скорости мины. Напомним, что этой траектории соответствует угол ?=45°. Нетрудно убедиться, что начальные скорости, соответствующие другим траекториям, монотонно возрастают при удалении этих траекторий от выделенной как вверх, так и вниз. Поэтому, если стена окажется ниже выделенной траектории, то решение тривиально: именно эта траектория и удовлетворяет поставленным условиям. Если стена окажется выше, то искомая траектория проходит через верхний край стены. Вот и всё.

Теперь остается только записать эти рассуждения на математическом языке, т.е. получить выражение для начальной скорости и угла ? в каждом из этих случаев.

Прежде всего получим общее уравнение траекторий, проходящих через цель. Как мы уже знаем, уравнение траекторий, выходящих из начала координат, имеет вид:

(1)

Потребуем, чтобы эти траектории проходили через цель. Для этого положим в (1) y=0 при x=a+b:

(2)

Выражая из (2) начальную скорость v₀ и подставляя в (1), получим уравнение всех траекторий, проходящих через цель:

(3)

Придавая ? разные значения в пределах от 0 до ?/2, получаем все траектории, изображенные на рисунке.

Выделенная траектория получается при tg?=1:

(4)

Выясним теперь, при каком условии эта траектория проходит над стеной. Для этого найдем высоту h₁ точки траектории при x=a:

Таким образом, если высота стены h меньше, чем h₁, то искомая траектория определяется выражением (4), а соответствующая ей начальная скорость v₀ легко находится из уравнения (2) при tg?=1:

Это есть обычное соотношение между начальной скоростью и максимальной дальностью полета по горизонтали.

Определим теперь искомую траекторию, если стена выше выделенной траектории: h>h₁. Как уже отмечалось, в этом случае нужно найти траекторию, проходящую через верхний край стены, т.е. положить в (3) y=h при x=a:

откуда

Уравнение искомой траектории получим, подставив найденное значение tg?₁ в формулу (3):

Отметим, что для ответа на поставленные в задаче вопросы это уравнение нам не требуется, но оно дает возможность проследить, через какие точки мина летит к цели. Для нахождения соответствующей этой траектории начальной скорости нужно подставить полученное значение tg?₁ в уравнение (2):

Итак, резюмируя все изложенное, сформулируем ответ:

Полезно и в этой задаче рассмотреть предельные случаи. Не будем останавливаться на относительно мало интересных случаях, как, например, a=b (стена посредине между минометом и целью).

Бессмысленно полагать a=0 или b=0 при h?0, но несомненно представляет интерес случай, когда a и b одновременно стремятся к нулю (при h?0). В этом предельном случае требуется просто перебросить мину через стену. Ответ в это случае очевиден: стрелять нужно вертикально вверх (?=?/2), а начальная скорость .

Покажем, как получить этот результат из ответа к задаче. Здесь, конечно, нужно обращаться к случаю h>ab/(a+b). Полагая a=b и одновременно устремляя их к нулю, получим ???/2 и